调节效应的原理与 Stata 实操
方法文献来源
如果变量与变量的关系是变量的函数, 称为调节变量。就是说,与的关系受到第三个变量的影响。——温忠麟(2004)
根据温忠麟教授2004年发表在《心理学报》中《调节效应与中介效应的比较和应用》提到的方法。双变量均为连续变量的情况下,一般通过分析交互效应来检验调节效应(Moderatoring)。直接来说,也就是观察:中,交互项的显著性有无作为调节效应有无判断的标准。
调节效应的Stata 实操
在进行调节效应的检验前,需要首先将自变量与调节变量进行中心化处理。

Stata 中若需要对变量进行中心化处理,则可以使用 Center 命令进行处理,此外,再构建自变量与调节变量中心化后的交互项。具体代码与执行结果如下:
centerd X M //中心化处理。其中,X为自变量;M为因变量。生成完成后,会生成附带`c_`前缀的变量。
(generated variables: c_X c_M)
gen W = c_X * c_M //意为生成变量名为W的交互项,代表中心化后的自变量与调节变量的乘积。生成后,则采用层次回归的方法进行检验。此时,将自变量、调节变量与生成的交互项交互项放入 回归中进行检验。不论是混合回归模型、随机效应模型或固定效应模型,均可以采用一样的形式进行回归,即:
reg Y X M W $$Controls , robust //其中,$$Controls代表使用global全局定义的控制变量;robust为采用稳健标准误。
reghdfe Y X M W $$Controls , absorb(id year) //采用固定效应模型的检验,同理。结果解读
在回归中加入调节变量后,主要关注交互项 ,也就是 的回归显著性。随后,将会输出结果如下:
. reg Y X M W,robust //加入中心化后的自变量、调节变量与二者的交叉项。
Linear regression Number of obs = 342
F(3, 338) = 746.05
Prob > F = 0.0000
R-squared = 0.8361
Root MSE = .64774
------------------------------------------------------------------------------
| Robust
Y | Coefficient std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
X | .5100745 .0268026 19.03 0.000 .4573536 .5627954
M | .291422 .0337473 8.64 0.000 .2250408 .3578031
W | .1776961 .0117229 15.16 0.000 .154637 .2007552
_cons | -.4102857 .1050263 -3.91 0.000 -.6168732 -.2036982
------------------------------------------------------------------------------其中,自变量、调节变量的显著性与方向在此时已经不再重要,而我们需要着重观察的,是交互项 ,也就是 的系数与显著性。由表格可知,交互项 (p<0.001,Coefficient=0.118)系数显著为正,因此判断为调节效应显著存在。
调节效应的报告
接下来,我们以发表在价格理论与实践(CSSCI&北核,影响因子:1.36)中的文章《人工智能对提升工作满意度的影响研究》为例,说明调节效应是如何在文中提出假设,以及如何将上述的表格进行报告。
调节效应的提出
调节效应存在的前提是主效应存在,在此,作者认为:劳动者在明确了解人工智能的角色和功能后,可以更有效地利用人工智能, 减少工作中的不确定性和潜在摩擦,从而提升协作满意度。提出:
H1:人工智能角色清晰度正向影响人机协作满意度。
其次,作者基于行动者网络理论进一步提出:人工智能感知有用性,不仅增强了人机协作效能, 而且还可能提高劳动者对于合作的期望和积极性,从而增强角色清晰度对满意度的正向作用。因此,人工智能感知有用性作为行动者间加强信任和减少抵抗的媒介,能够提升劳动者对人工智能的认可和合作意愿及行动者在合作中的满意度。当人工智能的感知有用性较高时,人工智能角色清晰度与合作满意度之间的正向联系将被强化。

由此,提出:
H2:人工智能感知有用性会正调节人工智能角色清晰度与人机协作合作满意度之间的关系。
调节效应的检验与报告
初步检验
限于篇幅原因,这里着重说明前文中描述的主效应与调节效应的检验。可以看到在下表的模型2中,作者将人工智能角色清晰度作为自变量对人机协作满意度作为因变量进行回归,系数显著为正(p<0.001,Coefficient=0.482),因此认为主效应显著存在。
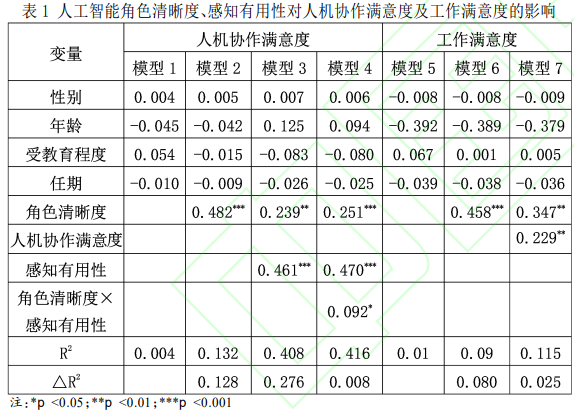
对于调节效应,则根据模型4的结果进行判断,可以看到,交互项的系数显著为正(p<0.05,Coefficient=0.092),因此可以判断为正向调节作用存在。此外,该研究的模型3实际上并无非常强的存在意义。在调节效应的结果叙述中,作者描述如下:
3.调节效应:
为检验人工智能感知有用性的调节效应,将人工智能角色清晰度与人工智能感知有用性进行标准化处理,并构建两者交互项,通过逐步回归的方式将人工智能感知有用性与交互项纳入回归方程。如表 1 模型 3 所示,在控制人口统计学变量与任期及人工智能角色清晰度后,人工智能感知有用性对人机协作满意度 (模型 3,beta=0.461, p<0.001)的正向影响显著。随后,如表 1 中模型 4 所示,在回归中加入人工智能角色清晰度与人工智能感知有用性的交互项后,人工智能角色清晰度对人机协作满意度 (模型 4,beta=0.251, p<0.001)的正向影响仍显著,人工智能角色清晰度与人工智能感知有用性的交互项对人机协作满意度(模型 4,beta=0.092,p<0.05)的正向影响显著。由此,人工智能感知有用性正向调节了人工智能角色清晰度与人机协作满意度之间的 关系,假设 2 得到初步支持。
实际上假设2到此已经完全验证,因为调节效应并不如中介效应一般,检验方法存在极强的争论。一般来说,作为大部分情况下而言,到此可以说调节效应是显著存在的。
进一步检验
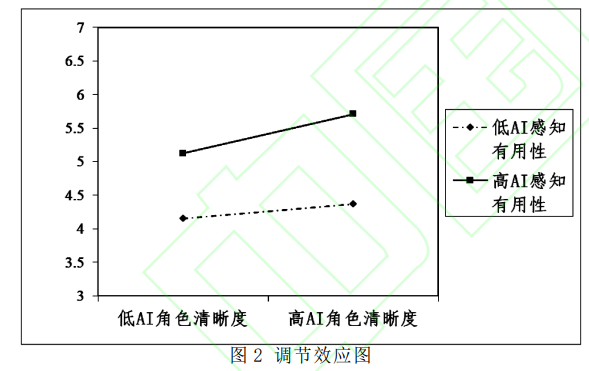
再进一步检验中,作者参考Aiken 等人(1991)的建议,以均值加减一个标准差为基准, 将人工智能感知有用性划分为高低水平,分别就人工智能角色清晰度和人机协作满意度进行回归分析。(实际上,这种方法在 Stata 中无法直接实现,一般通过 SPSS Process 中的 J-N 图选项进行实现)
此外,作者还进行了简单斜率检验,以此来进一步说明调节效应的调节方向。由图 2 可以发现,人工智能感知有用性越高,人工智能角色清晰度对人机协作满意度正向影响越大。到这里,调节效应的报告告一段落,假设二得到了完全的验证。
总结
总的来说,调节效应作为一种最常见的机制而言,在心理学和经济学等研究领域中被广泛使用。而需要注意的是,在经济学的研究中,研究者通常不会展示 J-N 图与简单斜率分析图,取而代之的,是直接通过表格进行展示,例如在机制分析表格中,通过直接添加交互项进入模型,来说明调节机制的存在;而在心理学中,研究者一方面处于审稿人的要求,另一方面则是作为领域研究的“惯习”而加入额外的图形检验。
但不论如何,需要强调的是,调节效应的核心依然是在中,通过交互项的显著性作为标准来进行研究的。此外,值得一提的是,在经济学的研究中,为了说明调节效应会为部分路径的系数带来质的变化,研究者有时会通过 bdiff 命令来检验组间系数差异。
参考文献:
[1]温忠麟,侯杰泰,张雷.调节效应与中介效应的比较和应用[J].心理学报,2005(02):268-274.
[2]程建华,武星.人工智能对提升工作满意度的影响研究[J/OL].价格理论与实践:1-6[2024-03-14].2023.12.471.
[3]Aiken L S. Multiple regression: Testing and interpreting interactions [J]. Sage google schola, 1991, 2: 103-135.